Introduzione
Dedicheremo questo nuovo capitolo allo studio delle programmazioni logica e funzionale in Python. Questi due paradigmi di programmazione sono alla base della programmazione nell’Intelligenza Artificiale (IA) e costituiscono i primi esempi di codice che apprende da insiemi di schemi e regole. La programmazione Logica riguarda lo studio dei principi che definiscono il processo di ragionamento e consiste nell’analisi delle regole attraverso le quali è possibile inferire dei risultati. Ad esempio, a partire da tre affermazioni con valore “Vero”, un programma può inferire il risultato di una quarta espressione correlata.
Descrizione dell’idea
La programmazione logica, come si può intuire dal nome, è una combinazione di due diversi concetti: la logica e la programmazione. La logica si usa per descrivere i fatti e le regole che devono essere interpretati dal programma. Un approccio logico alla programmazione richiede un insieme di regole in input che il programma deve apprendere per inferire un certo risultato a partire da un nuovo fatto mai visto prima. La programmazione logica può anche essere vista come una forma di apprendimento con l’uso esplicito di istruzioni di supporto all’apprendimento.
Cos’è la programmazione logica?
Scrivendo codice in Python, C, C++, Java o altro ancora, sappiamo bene che esistono diversi paradigmi di programmazione, come quello orientato agli oggetti (OOP), astrazioni, costrutti iterativi e molte altre istruzioni tipiche della programmazione. La Programmazione Logica è semplicemente un altro di questi paradigmi che lavora su relazioni. Tali relazioni vengono definite attraverso fatti e regole memorizzate all’interno di un database relazionale. Questo paradigma si basa su eventi espressi in logica formale ed esplicita.
Relazioni
Le relazioni costituiscono le basi della programmazione logica. Una relazione può essere definita come un fatto che segue una certa regola. Ad esempio, la relazione [ A -> B ] si legge “se A è vero, B è vero”. In altri termini, possiamo leggere la precedente relazione come “Se sei un Ingegnere, allora sei anche un Laureato”, il che porta a dedurre che “Gli Ingegneri sono Laureati”. A seconda del linguaggio di programmazione usato, la semantica delle relazioni cambia in base alla sintassi del linguaggio ma l’idea alla base delle relazioni è la stessa.
Fatti
Qualsiasi programma basato sulla logica ha bisogno di fatti, bisogna cioè fornire al programma dei fatti in modo da raggiungere un obiettivo specifico. Come suggerisce anche il nome, un fatto definisce ciò che è vero. I dati e i programmi, nella logica, sono quindi rappresentati da affermazioni di verità. Ad esempio, un fatto è che Washington è la capitale degli USA.
Regole
Le regole sono quei vincoli che aiutano a trarre delle conclusioni a partire da un dominio. Le regole sono clausole logiche di cui un programma o un fatto si serve per definire delle relazioni. Per avere un’idea, prendiamo un fatto: Raman è un uomo. Ora, possiamo considerare una regola sul genere, essendo questo un’entità singola: un uomo non può essere una donna. Per cui, a partire dal fatto che Raman è un uomo, si può costruire la relazione che Raman, essendo un uomo, non può essere una donna. Vediamo come vengono costruite le regole:
Ad esempio: antenato(A,B) :- genitore(A,B).
antenato(A,C) :- genitore(A,B), antenato(B,C).
Quanto sopra può essere letto come: per ogni A e B, se A è genitore di B e B è antenato di C, A è antenato di C. Oppure, per ogni A e B, A è antenato di C se A è genitore di B e B è antenato di C.
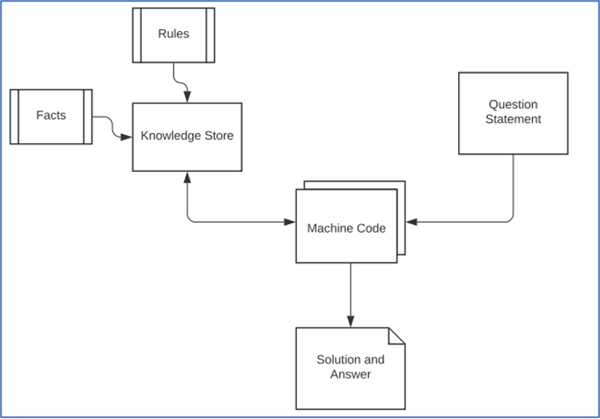
Casi d’uso di Programmazione Logica
- La programmazione Logica è ampiamente usata nel Natural Language Processing (NLP) dal momento che la comprensione del linguaggio riguarda il riconoscimento di schemi che non si possono rappresentare coi numeri;
- si usa anche nella modellazione di prototipi, dal momento che si può semplificare la prototipazione usando la logica per replicare espressioni e schemi;
- la programmazione logica viene anche usata per il riconoscimento di pattern in algoritmi di elaborazione di immagini, speech recognition e altro;
- la programmazione logica permette anche di risolvere in maniera efficiente problemi di scheduling e allocazione delle risorse;
- infine, rende le dimostrazioni matematiche facili da decifrare.
Risolvere enigmi con l’Intelligenza Artificiale
La programmazione Logica si può impiegare per risolvere molti problemi matematici che possono essere di supporto alla costruzione di macchine intelligenti. Nella prossima sezione, vedremo come si può usare la programmazione logica per valutare espressioni matematiche e implementeremo un programma che apprende alcune operazioni per fare predizioni. Risolveremo anche un problema reale usando due librerie Python molto usate per la programmazione logica:
- Kanren: Kanren è una libreria di PyPi che semplifica l’integrazione della logica di business all’interno del codice. Con Kanren si possono codificare facilmente la logica, le regole e i fatti discussi in precedenza. Questa libreria usa forme avanzate di pattern matching per decifrare le espressioni in input e per costruire una propria logica. Nella prossima sezione useremo questa libreria per risolvere dei calcoli matematici. Nel prossimo segmento di codice vedremo come installarla e importarla nel nostro ambiente di sviluppo.
- SymPy: SymPy sta per “symbolic computation in Python” ed è una libreria open-source che serve a risolvere costrutti matematici tramite l’uso di simboli. La proposta del progetto SymPy è di creare un sistema di calcolo algebrico (Computer Algebra System – CAS) completamente funzionale con lo scopo di mantenere il codice totalmente comprensibile e semplice da usare.
# Eseguiamo il seguente comando per installare kanren, dal momento che non si trova preinstallato nella distribuzione che adoperiamo.
pip install kanren
>>>
Collecting kanren
Downloading kanren-0.2.3.tar.gz (23 kB)
Collecting unification
Downloading unification-0.2.2-py2.py3-none-any.whl (10 kB)
Building wheels for collected packages: kanren
Building wheel for kanren (setup.py): started
Building wheel for kanren (setup.py): finished with status 'done'
Installing collected packages: unification, kanren
Note: you may need to restart the kernel to use updated packages.
Successfully installed kanren-0.2.3 unification-0.2.2
# Una volta installato kanren, installiamo anche sympy.
pip install sympy
Una volta installate le librerie siamo pronti a implementare la programmazione logica in Python. Iniziamo col calcolare alcune funzioni matematiche.
Programmazione Logica per la valutazione di assiomi matematici
Gli algoritmi non fanno altro che implementare e controllare la logica. Allo stesso modo, un’espressione matematica è logica applicata alle funzioni. Queste espressioni costituiscono l'input di un programma e vengono quindi usate dal programma per dedurre le regole espresse all’interno della logica. Sulla base della comprensione di tali regole si possono valutare nuove espressioni. Vediamo come implementare la programmazione logica per valutare espressioni matematiche:
# Importiamo le funzioni necessarie dalla libreria kanren
from kanren import run, var, fact
from kanren.assoccomm import eq_assoccomm as eq
from kanren.assoccomm import commutative, associative
# Definiamo i valori per eseguire le operazioni di addizione e moltiplicazione
addition = 'add'
multiplication = 'mul'
# Per ciascuna operazione definiamo i fatti e le proprietà
fact(commutative, multiplication)
fact(commutative, addition)
fact(associative, multiplication)
fact(associative, addition)
# Dichiariamo le variabili che formeranno l’espressione
var_x, var_y, var_z = var('var_x'), var('var_y'), var('var_z')
# Costruiamo un pattern corretto che il programma dovrà apprendere
match_pattern = (addition, (multiplication, 4, var_x, var_y), var_y, (multiplication, 6, var_z))
match_pattern = (addition, (multiplication, 3, 4), (multiplication, (addition, 1, (multiplication, 2, 4)),2))
# Costruiamo 3 espressioni per verificare l’apprendimento della funzione
test_expression_one = (addition, (multiplication, (addition, 1 , (multiplication, 2, var_x )), var_y) ,(multiplication, 3, var_z ))
test_expression_two = (addition, (multiplication, var_z, 3), (multiplication, var_y, (addition, (multiplication, 2, var_x), 1)))
test_expression_three = (addition, (addition, (multiplication, (multiplication, 2, var_x), var_y), var_y), (multiplication, 3, var_z))
# Valutiamo le espressioni di test
run(0,(var_x,var_y,var_z),eq(test_expression_one,match_pattern))
>>> ((4, 2, 4),)
run(0,(var_x,var_y,var_z),eq(test_expression_two,match_pattern))
>>> ((4, 2, 4),)
print(run(0,(var_x,var_y,var_z),eq(test_expression_three,match_pattern)))
>>> ( )
# Le prime due soddisfano l’espressione, infatti ritornano i valori delle singole variabili, mentre la terza espressione, avendo una struttura differente, non genera alcuna corrispondenza
# Eseguiamo delle valutazioni matematiche con SymPy
import math
import sympy
print (math.sqrt(8))
>>> 2.8284271247461903
# Nonostante la funzione radice quadrata di Math fornisca in output la radice quadrata di 8, sappiamo che questo è un risultato approssimato, dal momento che la radice quadrata di 8 è un numero reale ricorsivo e infinito.
print (sympy.sqrt(3))
>>> sqrt(3)
# Al contrario, SymPy ritorna un simbolo, che indica la reale radice di 3
# Nel caso di radici quadrate semplici, come la radice di 9, SymPy ritorna il risultato corretto e non una risposta simbolica
Questi sono solo alcuni casi d’uso di base per imparare a usare le librerie di programmazione logica. Vedremo più a fondo questi concetti nei capitoli sul Natural Language Processing (NLP) e sullo Speech Recognition di questo tutorial. Per ora, vediamo ancora come risolvere la ricerca di numeri primi in Python.
# Importiamo le librerie necessarie a eseguire la funzione Prime Number
from kanren import membero, isvar, run
from kanren.core import goaleval, condeseq, success, fail, eq, var
from sympy.ntheory.generate import isprime, prime
import itertools as iter_one
# Definiamo una funzione per la costruzione dell’espressione
def exp_prime (input_num):
if isvar(input_num):
return condeseq([(eq, input_num, x)] for x in map(prime, iter_one.count(1)))
else:
return success if isprime (input_num) else fail
# Variabili da usare
n_test = var()
set(run(0, n_test,(membero, n_test,(12,14,15,19,21,20,22,29,23,30,41,44,62,52,65,85)),( exp_prime, n_test)))
>>> {19, 23, 29, 41}
run(7, n_test, exp_prime(n_test))
>>> (2, 3, 5, 7, 11, 13, 17)
Implementare la programmazione logica in Python permette ai programmatori di eseguire operazioni matematiche complesse direttamente nel codice. Molte applicazioni discusse in precedenza si basano sulla programmazione logica, vedremo come usarne alcune nei prossimi capitoli. Intanto, esploriamo un altro paradigma importante per lo sviluppo di applicazioni intelligenti: la programmazione Funzionale.
Programmazione Funzionale in Python
La programmazione funzionale è un approccio dichiarativo di scrittura del codice che si basa su “ciò che deve essere risolto” piuttosto che sul “come risolverlo”. Per costruire il codice, non si usano istruzioni ma espressioni. Mentre l’esecuzione di un’istruzione assegna delle variabili, risolvere un’espressione significa assegnare dei valori. La programmazione Funzionale si basa sui seguenti concetti:
- Funzioni pure: sono funzioni strettamente orientate al risultato. L’idea è che input uguali producono sempre lo stesso output indipendentemente da qualsiasi altra condizione nel codice. Inoltre, le funzioni pure non hanno effetti collaterali sul codice, cioè non modificano argomenti o variabili globali.
- Ricorsione: nella programmazione funzionale non esistono costrutti come i cicli while e i cicli for, perché tutte le iterazioni si calcolano usando la ricorsione.
- Funzioni di prima classe e di ordine superiore: tutte le variabili di prima classe di una porzione di codice funzionale possono essere passate come argomenti a funzioni di prima classe. I parametri di queste funzioni vengono memorizzati all’interno di strutture dati usate dalla funzione per restituire l’output.
- Variabili immutabili: tutte le variabili di un programma funzionale non possono essere modificate dopo la loro inizializzazione. È comunque sempre possibile creare nuove variabili.
# Lavoriamo con le funzioni pure in Python
# Una funzione pura non modifica la lista in input
def pure_func(List):
Create_List = []
for i in List:
Create_List.append(i**3)
return Create_List
# Esempio
Initial_List = [1, 2, 3, 4]
Final_List = pure_func(Initial_List)
print("The Root List:", Initial_List)
print("The Changed List:", Final_List)
>>> The Root List: [1, 2, 3, 4]
>>> The Changed List: [1, 8, 27, 64]
# Implementiamo la ricorsione in Python per sommare gli elementi di una lista
def Sum(input_list, iterator, num, counter):
if num <= iterator:
return counter
counter += input_list[iterator]
counter = Sum(input_list, iterator + 1, num, counter)
return counter
# Esempio
input_list = [6, 4, 8, 2, 9]
counter = 0
num = len(input_list)
print(Sum(input_list, 0, num, counter))
>>> 29
# Dimostrazione dell’uso di funzioni di ordine superiore in Python
def func_shout(text_input):
return text_input.upper()
def func_whisper(text_input):
return text_input.lower()
def greet(func_var):
# Memorizziamo la funzione come una variabile
greet_text = func_var("Hello, I was passed like an argument to a function")
print(greet_text)
greet(func_shout)
greet(func_whisper)
>>> HELLO, I WAS PASSED LIKE AN ARGUMENT TO A FUNCTION
>>> hello, i was passed like an argument to a function
Vediamo alcune funzioni chiave di ordine superiore. La programmazione funzionale usa alcune funzioni di ordine superiore predefinite per implementare il calcolo di oggetti iterabili come liste, dizionari, tuple, ecc.... Alcune di queste sono implementate in seguito:
map(): la funzione map() in Python ritorna una lista di risultati ottenuti dopo aver applicato una funzione a tutti i membri di un oggetto iterabile;filter(): la funzione filtro è una funzione booleana che verifica alcune condizioni predefinite su tutti gli elementi di un oggetto iterabile;- Funzioni
lambda: le funzioni lambda in Python sono funzioni anonime, cioè che non hanno un nome e che quindi non vengono dichiarate con la parola chiave def, ma che vengono definite con la parola lambda.
# Implementazione della funzione Map() in Python
def addition(num):
return num + num
# Implementiamo una funzione che raddoppia i numeri di una tupla
input_numbers = (3, 4, 1, 2)
final_results = map(addition, input_numbers)
# L’istruzione seguente non ritorna il risultato ma mostra solo il tipo dell’oggetto
print(final_results)
# Per stampare il risultato eseguiamo:
for num_result in final_results:
print(num_result, end = " ")
>>>
>>> The extracted vowels are:
>>> a
>>> i
>>> e
# Implementazione della funzione Filter()
# Definiamo una funzione per filtrare le vocali di una lista
def Check_Vowel(var):
vowels = ['a', 'e', 'i', 'o', 'u']
if (var in vowels):
return True
else:
return False
test_seq = ['m', 'a', 'i', 'x', 'q', 'd', 'e', 'k']
filter_output = filter(Check_Vowel, test_seq)
print('The extracted vowels are:')
for s in filter_output:
print(s)
>>> 512
>>> [4, 2, 6]
Importanza della programmazione Logica e Funzionale per l’IA
La Programmazione Funzionale si distingue nel garantire la costruzione di programmi fault-tolerant per effettuare velocemente calcoli lunghi e critici, il che semplifica i processi decisionali. La tolleranza ai guasti e la rapida formulazione delle decisioni rendono la programmazione funzionale molto importante per l’IA. Sebbene al momento non venga sfruttato tutto il suo potenziale, la programmazione funzionale potrebbe, ad esempio, rendere le auto a guida autonoma più affidabili e sicure in futuro. In qualsiasi scenario che coinvolga la vita umana, infatti, un fallimento di un sistema potrebbe provocare effetti negativi, per questo la tolleranza ai guasti è un aspetto molto importante e il concetto della programmazione funzionale che rende i sistemi più affidabili è l’immutabilità. Inoltre, la Lazy Evaluation consente di risparmiare memoria in modo da velocizzare i processi. Anche la programmazione parallela migliora l’efficienza delle macchine, mentre l’idea di poter passare funzioni come argomenti ad altre funzioni aumenta complessivamente la funzionalità del sistema. Tutte queste caratteristiche della programmazione funzionale la rendono particolarmente adatta all’intelligenza artificiale.
La Programmazione Logica, d’altro canto, aiuta gli agenti intelligenti nello svolgimento di operazioni ripetitive e che si verificano spesso, lasciando la possibilità di effettuare analisi a partire da queste operazioni. L’analisi inferenziale, che è una proprietà del linguaggio, riduce il gap con l’analisi logica ad alto livello e la sua implementazione rappresenta un caso d’uso in cui la programmazione logica migliora le funzionalità degli algoritmi di IA. Il codice basato sulla logica utilizza un approccio di programmazione dichiarativo, che si concentra sul rendere il codice leggibile e simile alla lingua inglese. D’altronde, l’intelligenza artificiale mira a implementare macchine che imitino l’intelligenza umana. La programmazione logica fornisce a queste macchine il potere di ragionamento, consentendo loro di fare ragionamenti inferenziali come gli esseri umani.
Prossimamente...
Con questo tutorial siamo entrati in contatto con la programmazione logica, la programmazione funzionale e la loro importanza nella realizzazione di algoritmi di IA. Esistono diversi esempi avanzati di utilizzo di questi paradigmi di programmazione che vengono spesso usati in teoria dei gruppi, natural language processing e altro ancora. Nei prossimi capitoli approfondiremo la programmazione logica per gli algoritmi di scienza cognitiva.
Di seguito, alcuni argomenti che tratteremo a seguire:
- Natural Language Processing;
- Tokenizzazione, Stemming e Lemmatizzazione;
- Text Mining.